From June 19-23, 2023, the Vietnam Institute for Advanced Study in Mathematics (VIASM) in collaboration with the Institute of Mathematics (Vietnam Academy of Science and Technology) held a Commutative Algebra and its interaction with Algebraic Geometry and Combinatorics 2023. The conference is a place to discuss some recent new results as well as future research directions with issues arising from them. This is suitable and very urgent for the majors in Mathematics related to the conference topic.

Speakers and participants on the first day
The conference program took place in 5 days with 28 reports from Hanoi University of Science and Technology, University of Science - Thai Nguyen University, University of Missouri (USA), Dalhousie University (Canada), University of Barcelona (Canada). Spain) etc.
The conference attracted more than 50 scientists from many domestic and foreign universities. Tran Nam Trung (Institute of Mathematics), Prof. Ha Huy Tai (Tulane University, USA), Prof. Dao Hai Long (University of Kansas, USA), Prof. Steven Dale Cutkosky (USA), Prof. Marc Chardin (France), etc.
In particular, the conference gave young researchers the opportunity to listen and talk directly with experts in the field of commutative algebra.

Prof. Le Tuan Hoa, at the Opening ceremony.
Opening the conference, Prof. Bernd Ulrich (Purdue University) reported on a partial solution to the problem of finding equations defining the image and the graph of a morphism between projective spaces. The problem of finding defining equations from parameterization (the implicitization problem) is one of the classical problems of algebraic geometry. Using newly developed tools such as Jouanolou duality for a class of generalized Gorenstein rings, Prof. Ulrich and colleagues have solved a new families of implicitization problems
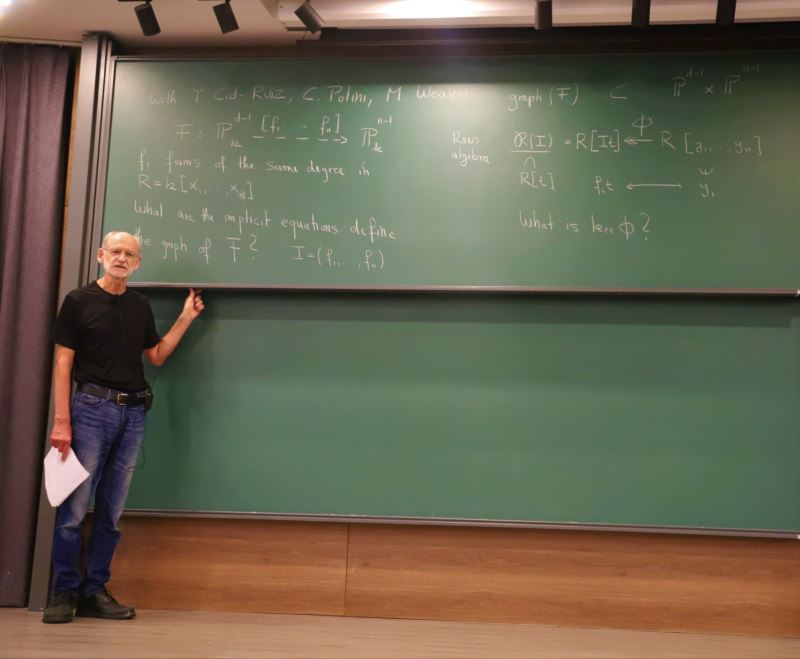
Prof. Bernd Ulrich (Purdue University, USA) speaks on a partial solution to the problem of finding equations defining the image and graph of a morphism between projective spaces.
On the occasion of Prof. Ngô Việt Trung's 70th birthday, Prof. Hà Huy Tài (Tulane University) gave a lecture on the Castelnuovo--Mumford regularity of graded families of homogeneous ideals in a polynomial ring. The lecture focuses on the contributions of Prof. Ngô Việt Trung to the study of regularity of powers of an ideal and the subsequent work influenced by the pioneering research of Trung and his coauthors such as J. Herzog, Cutkosky, and other leading experts such as Kodiyalam, Bertram, Ein, Lazarsfeld,.... Research on the regularity of powers of ideals has developed into an important research direction, incorporating various techniques from commutative algebra, algebraic geometry, graph theory, and many intriguing problems remain unsolved in this exciting line of research.

Prof. Hà Huy Tài (Tulane University, USA) delivers his invited lecture on the Castelnuovo--Mumford regularity of graded families of homogeneous ideals at the conference.
Studying the behavior of algebraic and geometric invariants under flat base changes is a classic method that was pioneered by Grothendieck and has had a profound influence on algebraic geometry. In the lecture of Prof. Lê Thanh Nhàn, this research direction continues to be deepened with the focus on the liftability of module structure along a ring map and the behavior of the attached primes of the local cohomology modules.

Prof. Lê Thanh Nhàn (Ministry of Education and Training) delivers a lecture on the behavior of Artinian local cohomology modules under flat base change.
The rate of a standard graded algebra R over a field K measures the deviation of R from being a Koszul ring. Koszul K-algebras are precisely the algebras with the minimal possible rate, namely 1. Generic Gorenstein algebras of socle degree 3 are always Koszul. In her lecture, Prof. Maria E. Rossi discussed a beautiful generalization of the above result, namely generic Gorenstein algebras of socle degree s at least 3 have the rate being precisely the floor of s/2. The new results of Rossi and her colleagues also provide interesting information about the free solutions of generic Gorenstein algebras.

Prof. Maria Evelina Rossi (University of Genoa, Italy) lectures on the rate of generic Gorenstein algebras over a field.
At this conference, Prof. Marc Chardin (Sorbonne University) gave a lecture on the support of Tor modules and multigraded local cohomology. The new results of Prof. Chardin and his coauthor provide interesting information about linear resolutions of truncations and the regularity of powers of ideals.

Prof.. Marc Chardin (Sorbonne University, France) reports on standard multigraded torsion modules and local cohomology.
The Hilbert-Kunz multiplicity, defined in terms of the Frobenius map, is an important invariant in the study of rings of positive characteristics. The Hilbert-Kunz multiplicity plays a similar role as the Hilbert-Samuel multiplicity of a local ring. At this conference, Prof. Jugal Verma (Indian Institute of Technology, Mumbai) gave a lecture on the Hilbert-Kunz multiplicity of powers of an m-primary ideal. Ilya Smirnov recently proposed a tantalizing conjecture connecting the Hilbert-Kunz multiplicity of powers of an m-primary ideal to the Hilbert coefficients of the Frobenius powers of that ideal. The lecture of Prof. Verma provides the audience with a broad context full of interesting and surprising results related to Smirnov's conjecture. The lecture concluded with a solution of a non-trivial case of Smirnov's conjecture.

Prof. Jugal Verma (Indian Institute of Technology, Mumbai) reports on a conjecture due to Ilya Smirnov on the Hilbert-Kunz multiplicity of powers of an ideal.

The participants at the tea breaks

