Vietnam Institute for Advanced Study in Mathematics (VIASM) successfully organized the Winter school on Representation theory and combinatorics tools in the study of some probabilistic models in Ha Noi from December 02 to December 04, 2024. This is a collaborative event between VIASM and the Vietnam-France International Research Laboratory in Mathematics and Applications (IRL FVMA) on the occasion of Prof. Kilian Raschel's visit to the Institute in 6 months.
 GS. Kilian Raschel - CNRS and University of Angers, France gave an opening speech
GS. Kilian Raschel - CNRS and University of Angers, France gave an opening speech
The winter school attracted more than 60 participants, including undergraduate, graduate students, lecturers, and professors from Vietnam and abroad (Thailand, India). The organizing committee sponsored 05 domestic participants outside Ha Noi to attend the winter school.
The winter school consisted of 4 special topic courses with 8 lectures delivered by world leading experts on Representation theory and combinatorics tools in the study of some probabilistic models: Prof. François Chapon (University of Toulouse, France), Prof. Cédric Lecouvey (University of Tours, France), Prof. Marc Peigné (University of Tours, France) and Prof. Sandro Franceschi (Télécom SudParis/Institut Polytechnique de Paris, France). The lectures at the winter school focused on many current issues in Winter school on Representation theory and combinatorics tools in the study of some probabilistic models.
The lectures at the school focus on exploring the Pitman transform for random processes through various approaches, such as Doob's transformation, harmonic analysis, representation theory, and combinatorial methods.
 Prof. Marc Peigné (University of Tours, France)
Prof. Marc Peigné (University of Tours, France)
Professor Marc Peigné gave a lecture on Pitman theorem for simple random walks on Z^d. He proved with elementary arguments that (S(n) − M(n)), with S(0) = 0 and M(n) = max(S(k) | 1 ≤ k ≤ n), is a Markov chain on Z+, whose transition function p(x, y) can be computed. This transition probability is expressed as the Doob transform of the transitions of the simple random walk, obtained using a positive harmonic function of this random walk confined to Z+. The Pitman transform therefore proposes a trajectory interpretation of this Doob transform and can be extended in higher dimensions.

Prof. Sandro Franceschi (Télécom SudParis/Institut Polytechnique de Paris, France)
Professor Sandro Franceschi delivered a lecture on Lévy representation for reflected Brownian motion and Pitman theorem for 3D Bessel process. Lévy's representation theorem establishes that a reflected Brownian motion, which is the absolute value of a Brownian motion noted |W(t)|, is equal in law to a Brownian motion B(t) minus its infimum before time t, noted I(t). Pitman's representation theorem states that a Brownian motion conditioned to remain positive, which is a 3-dimensional Bessel process, is equal in law to a Brownian motion B(t) minus twice its infimum I(t). In this talk Sandro Franceschi first introduced some notions of stochastic calculus such as local times, Bessel processes, and Doob's h-transforms, which will then allow him to present these two theorems and provide sketches of their proofs. This talk presented a continuous version in dimension 1 of the results presented by Marc Peigné in his talk on a discrete version of Pitman’s theorem for random walks in Z^d.
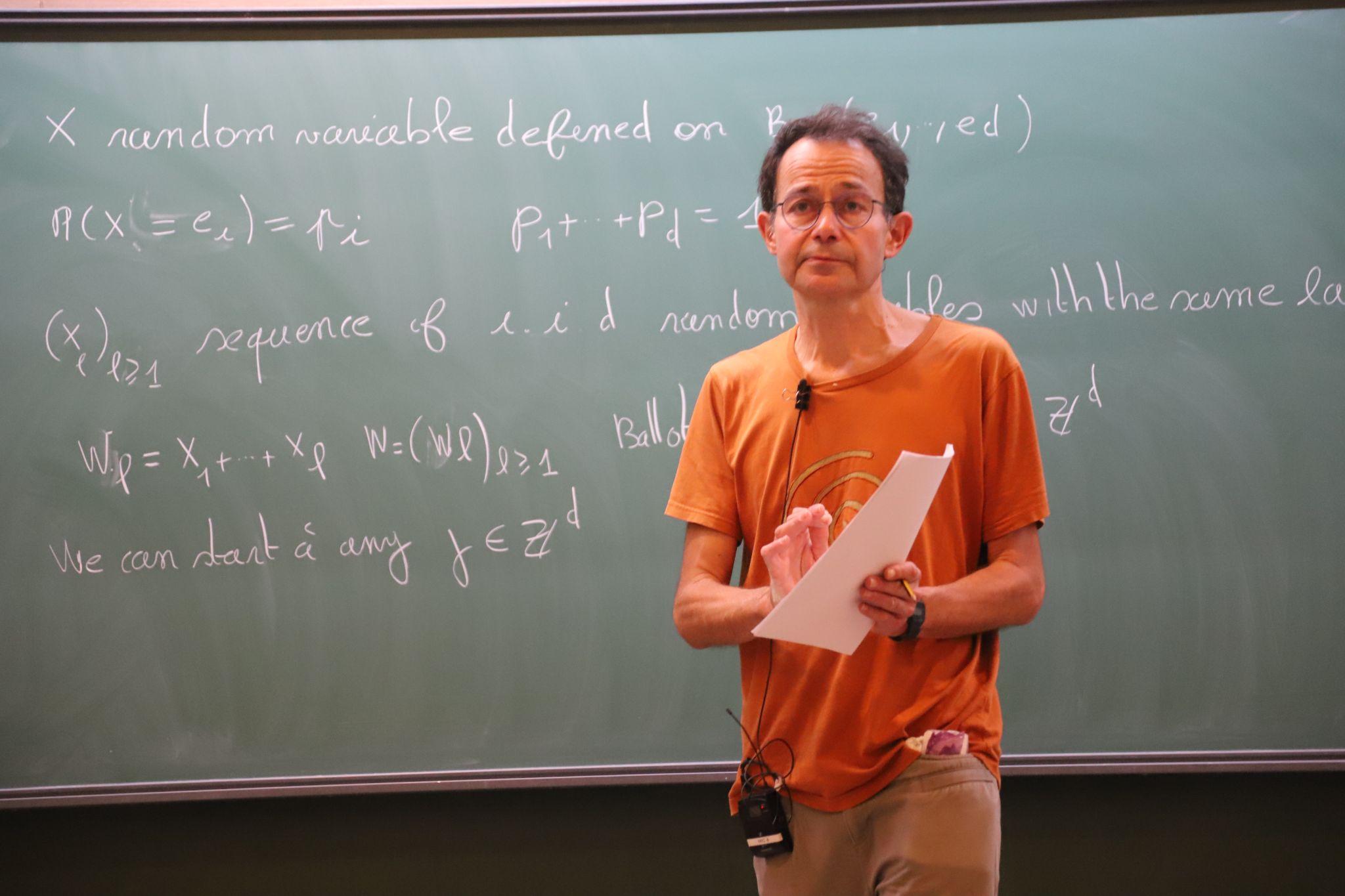
Prof. Cédric Lecouvey (University of Tours, France)
Professor Cédric Lecouvey gave a topic course on the interaction between representation theory of simple Lie algebras and ballot random walks on Z^d. The mini-course was concerned with interactions between representation theory of simple Lie algebras and certain random walks defined on lattices in Euclidean spaces. The mini-course started with the so-called “ballot random walk” which is related to the representation theory of sl(n). In this case, the Pitman transformation P is based on the Robinson-Schensted-Knuth correspondence which maps the words on the ordered alphabet (regarded as finite paths in R^d) on pairs of semistandard tableaux and can be regarded as a d-dimensional analogue of the celebrated Pitman transform. The results can be extended to a large class of random walks defined from representations of Lie algebras (or their generalizations known as Kac-Moody algebras). The corresponding transformation P is then defined in terms of the Littelmann path model. In the opposite direction, the probabilistic approach can be used to obtain asymptotic behavior of tensor product multiplicities.

Prof. François Chapon (University of Toulouse, France)
François Chapon gave a mini-course on non-commutative probability, representation theory and the orbit method. Pitman's theorem states that a Brownian motion minus twice its running infimum enjoys the Markov property. The aim of this mini-course is to understand this theorem through the lens of non-commutative probability. Non-commutative probability generalizes classical probability by replacing the algebra of bounded random variables with a non-commutative algebra of observables, for instance the universal enveloping algebra U(sl(2)) of the Lie algebra sl(2). Since the seminal works of Biane, it is now understood that Pitman's theorem is intimately related to the representation theory of a quantized deformation of the algebra U(sl(2)), in the so-called "crystal regime". On the other hand, Bougerol and Jeulin showed the appearance of the same Pitman transform in the infinite curvature limit of a Brownian motion on the symmetric space SL2(C)/SU(2). François Chapon presented a unified point of view of these two approaches by considering curvature deformation and semi-classical limit of the algebra U(sl(2)). This can be viewed as a probabilistic implementation of Kirillov’s orbit method. This course was self-contained, beginning with an introduction to non-commutative probability and how one can construct dynamics governed by the tensor product of irreducible representations of sl(2). All necessary algebraic and probabilistic notions were reviewed.
The lectures were carefully prepared to make it as easy as possible for senior undergraduate and graduate students to access abstract and modern mathematical knowledge. The participants actively engaged with the speakers through numerous questions, discussions, and exchanges.
Besides the lectures, there are four talks given by experts in Probability theory:

Assoc Prof. Ngo Hoang Long (University of Education) gave a talk titled “Strong solution and approximation of time-dependent radial Dunkl processes with multiplicative noise”.

Dr. Lam Hoang Chuong (Can Tho University) talked titled “Asymptotic behavior for one-dimensional random walks with external forces”.

Dr. Vu Thi Huong (University of Transport and Communications) delivered a talk titled “A tamed-adaptive Milstein scheme for stochastic differential equations with low regularity coefficients”.

Dr. Pham Viet Hung (Institute of Mathematics, Vietnam Academy of Science and Technology) presented a talk titled “Conjunction probability of Gaussian fields”.
The winter school was successfully organized and received much positive feedback from the participants. The event also served as an opportunity to strengthen exchanges and collaborations between the Vietnamese and international mathematics communities, helping to expand opportunities for students to study, work, and exchange knowledge.
Some photos from the winter school:






