SUMMER SCHOOL
Course 1: Biological propagation via reaction-diffusion equations with nonlocal diffusion and free boundary
Lecturers: Yihong Du, University of New England, Australia
Abstract: Spreading of biological species has been modeled by reaction-diffusion equations since the pioneering works of Fisher (1937) and KPP (Kolmogorov-Petrovsky-Piscunov, 1937). These classical models reveal an asymptotic spreading speed which agrees with observations of numerous real world examples. However, they do not provide enough information on the population range of the spreading species. This shortcoming can be eliminated by considering a corresponding free boundary problem, where the range boundary is represented by the free boundary. Moreover, to include more general dispersal strategies of the spreading species, such as long-distance dispersal, nonlocal diffusion has been introduced to these models in many recent works, and a new phenomenon, known as accelerated propagation, has been found in these nonlocal models. In this mini-course, I will look at some important models for propagation with nonlocal diffusion and free boundaries, starting with the basic properties of the equations, and progressing to some of the current topics on such models, including precise estimates of the rates of accelerated propagation.
Course 2: Age structured equations and travelling waves for systems arising in population dynamics
Lecturer: Arnaud Ducrot, Université Le Havre Normandie, France
Abstract: In these lectures, we will revisit important properties of linear semigroups, including their generation and key aspects of spectral theory. We will then discuss age-structured problems and the so-called integrated semigroup theory, which enables us to derive significant insights into the spectral theory of non-densely defined operators via the variation-of-constants formula.
In the second part of these lectures, we will explore propagation phenomena in time-heterogeneous reaction-diffusion systems, including traveling waves. This leads to the concepts of generalized traveling waves and spreading speeds.
Finally, we will combine age structure and diffusion to study the spatial propagation of oscillations. The analysis of this problem is carried out using integrated semigroup theory and bifurcation theory.
Course 3: Diffusion-induced spatially localized patterns in biological models
Lecturer: Yoshihisa Morita, Ryukoku University, Japan
Abstract: A variety of spatial patterns and pattern dynamics are observed in models in the fields of mathematical sciences. As such models, reaction-diffusion equations are widely used to describe pattern formation. Although the model equations are simple, they play a crucial role in understanding the mechanisms behind phenomena observed in the fields such as population biology,cell biology and physiology. In this series of lectures we will focus on the mathematical structures that induce pattern formation in reaction-diffusion equations. We will show how the reaction-diffusion equations, which are formulated simply by adding Laplacians to ordinary differential equations, exhibit rich solution structures in various situations. To this end, after preparing mathematical tools to analyze the solutions, such as basic theories of stability analysis, variational analysis and the comparison principle, we show how the existence of localized patterns in biological model equations can be proved mathematically. Topics include the bistable reaction-diffusion equation, the Lotka-Volterra competition-diffusion system, the FitzHugh-Nagumo system and mass-conserved reaction-diffusion systems.
Course 4: Gaussian and Lévy dispersals for population dynamics
Lecturer: Enrico Valdinoci, University of Western Australia, Australia
Abstract: We explore various aspects of the logistic equation and other equations related to population dynamics, focusing on species employing different dispersal strategies, such as classical random walks, Lévy flights, and more. The advantages and disadvantages of these diffusion strategies for species survival are analyzed under various perspectives.
Workshop Plenary Speakers
Nguyễn Hữu Dư, VNU University of Science, Vietnam
Title: Analysis of Reaction-Diffusion Predator-Prey System under Random Switching
Abstract: This paper examines the asymptotic behavior of a spatially diffusive predator-prey model influenced by random Markovian switching
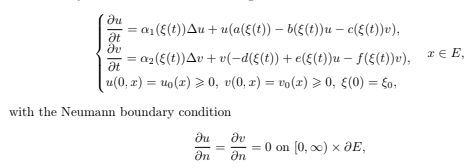
The system is formulated as a hybrid partial differential equation (PDE) with stochastic switching mechanisms. Then, a critical threshold is established to distinguish conditions leading to either species extinction or persistence. Moreover, we provide a comprehensive analysis of the ω-limit set, offering a pathwise characterization of the systems dynamics over time. Numerical simulations are also given to illustrate theoretical results. To the best of our knowledge, this is the first study to explore the predator-prey model within a framework that captures both spatial heterogeneity and switching randomness.
Serena Dipierro, University of Western Australia. Australia
Title: The Lévy flight foraging hypothesis
Abstract: We consider a forager diffusing via a fractional heat equation and we introduce several efficiency functionals whose optimality is discussed in relation to the Lévy exponent of the evolution equation. Several biological scenarios, such as a target close to the forager, a sparse environment, a target located away from the forager and two targets are specifically taken into account. The optimal strategies of each of these configurations are analyzed explicitly also with the aid of some special functions of classical flavor and the results are confronted with the existing paradigms of the Lévy foraging hypothesis. Interestingly, one discovers bifurcation phenomena in which a sudden switch occurs between an optimal (but somehow unreliable) Lévy foraging pattern of inverse square law type and a less ideal (but somehow more secure) classical Brownian motion strategy. Additionally, optimal foraging strategies can be detected in the vicinity of the Brownian one even in cases in which the Brownian one is pessimizing an efficiency functional.
Hoàng Thế Tuấn, Institute of Mathematics, Vietnam Academy of Science and Technology, Vietnam
Title: Qualitative Analysis of Incommensurate Fractional-Order Systems: Selected Topics and Applications
Abstract: In this report, we introduce and examine several fundamental problems in the qualitative theory of incommensurate fractional-order systems. Particular attention is given to recently developed analytical approaches and research techniques for integro-differential equations involving singular kernels. The discussion aims to highlight both theoretical advancements and their potential applications.
Phan Văn Tuộc, University of Tennessee, USA
Title: On Krylov-Safonov Harnack inequality for a class of parabolic equations with singular degenerate coefficients and related results.
Abstract: We discuss a class of linear parabolic equations in non-divergence form in which the leading coefficients are measurable, and they can be singular or degenerate as a weight that belongs to a class of Muckenhoupt weights. Krylov-Safonov Harnack inequality for solutions is proved under some smallness assumption on a weighted mean oscillation of the weight. As corollaries, Holder regularity estimates of solutions with respect to a quasi-distance, and a Liouville type theorem are presented. A class of weighted parabolic cylinders and the smallness condition on the weighted mean oscillation of the weight through are introduced and from which several growth lemmas are established. Additionally, a perturbation method is used and the parabolic Aleksandrov-Bakelman-Pucci type maximum principle is applied to suitable barrier functions to control the solutions. At the end of the talk, we will also discuss some related regularity results in Sobolev spaces for the class of the equations and then pose some open research directions.
The talk is based on the joint work with S. Cho (Gwangju National University of Education), and J. Fang (University of Tennessee).
Gael Raoul, Ecole Polytechnique, France
Title: Propagation of pathogens in a heterogeneous environment and emergence of resistance strains
Abstract: We consider a population that is structured by a phenotypic trait and a spatial variable. We will consider three strains (ie three possible trait values): resistance to a treatment A, resistance to a treatment B and resistance to both A and B (with a fitness cost for that last one). The treatments A and B will be alternated in space, and analyse the effect of this spatial heterogeneity on the propagation of the pathogen population. Several propagation strategies can be used by the pathogen to propagate in space: the propagation can for instance be driven by a specialist type, or by the multi-resistant. Through the use of propagation speed argument, we are able to discuss the emergence of multi-resistant strains at the edge of an epidemics, and show that propagation situations are more favourable than steady scenarii for the development of multi-resistance. This work has been done in collaboration with Matthieu Alfaro, Sylvain Gandon and Quentin Griette.
Đinh Cao Duy Thiên Vũ, University of Delaware, USA
Title: Parameter estimation on growing phylogenetic trees
Abstract: Phylogenetics is the study of the evolutionary history and relationships among individuals or groups of organisms from molecular sequence data such as DNA. Such relationships are usually represented by phylogenetic trees: leaf-labeled trees equipped with non-negative branch lengths. Based on the phylogenetic tree, information about the ancestral states, evolutionary parameters, and gene function inference, among others, can also be retrieved and analyzed. Since evolution is a dominant theme in biological research, phylogenetics also plays an essential role in the understanding of biological systems.
In recent years, there have been many efforts in research in phylogenetics to understand the statistical properties of evolutionary processes on growing trees (i.e., when the number of taxa increases while the number of traits/sequence length is fixed). In most processes, correlations among the sampled data do not decay, invalidating the standard statistical assumptions. This moves the learning problem into a regime where classical tools such as the Law of Large Numbers and the Central Limit Theorem no longer hold, making many well-known statistical estimates inconsistent.
In this talk, I will outline the main challenges and distinctive characteristics of statistical learning of evolutionary-related correlated random variables, using the problem of estimating the transition rate of a two-state model on phylogenetic trees as the guiding example. The aim is to illustrate that in this new regime, the problems of parameter estimation and ancestral state reconstruction are inherently intertwined and may need to be solved together with the help of a new class of concentration inequalities and identifiability conditions.
Yao Yao, National University of Singapore, Singapore
Title: Suppression of chemotactic blow-up by active advection
Abstract: Chemotactic blow up in the context of the Keller-Segel equation is an extensively studied phenomenon. In recent years, it has been shown that when the Keller-Segel equation is coupled with passive advection, blow-up can be prevented if the flow possesses mixing or diffusion-enhancing properties, and its amplitude is sufficiently strong. In this talk, we consider the Keller-Segel equation coupled with an active advection, which is an incompressible flow obeying Darcy's law for incompressible porous media equation and driven by buoyancy force. We prove that in contrast with passive advection, this active advection coupling is capable of suppressing chemotactic blow up at arbitrary small coupling strength: namely, the system always has globally regular solutions. (Joint work with Zhongtian Hu and Alexander Kiselev).
Zhi-An Wang, The Hong Kong Polytechnic University, Hong Kong
Title: Boundary spike/layer solutions of chemotaxis models
Abstract: In this talk, we shall report some progress made on boundary spike or layer solutions of chemotaxis models with physical boundary conditions: zero-flux and Dirichlet mixed boundary conditions based on some real experiments. We exploit a variety of questions such as the existence and stability of boundary spike/layer solution, as well as the convergence of boundary layers for small diffusion and effect of boundary curvature on the boundary layer thickness.
Contributed Talks
Nguyễn Thị Vân Anh, Hanoi National University of Education, Vietnam
Title: Approximation of Allen-Cahn equations with noncontinuous initial conditions to mean-curvature flow
Abstract: The Allen–Cahn equation (after John W. Cahn and Sam Allen’s work) is a reaction–diffusion equation of mathematical physics which describes the process of phase separation in multi-component alloy systems, including order-disorder transitions. The relation between the Allen–Cahn equation and mean curvature flow has been an ongoing investigation for several decades. For well-prepared initial conditions, Evans, Soner, and Souganidis proved the convergence to the viscosity solution, Ilmanen showed convergence results to a Brakke flow, and many others. In this talk, I will consider the Allen-Cahn equation under the initial condition by a ‘signed function’ of a given set. The solvability of problems, the convergence to the mean curvature flows in both classical and weak sense are also discussed. This is a part of an ongoing research project with Giovanni Bellettini.
Đoàn Thái Sơn, Institute of Mathematics, Vietnam Academy of Science and Technology, Vietnam
Title: Pole placement theorem for linear time-varying control systems
Abstract: In the first part of the talk, we first review the pole placement theorem for linear control systems. The second part is devoted to presenting several results on necessary and sufficient conditions for assignability of Lyapunov spectrum and dichotomy spectrum for linear time-varying control systems. This is a joint work with Adam Czornik and Nguyen Thi Thu Suong.
Nguyễn Tiến Tài, VNU University of Science, Vietnam
Title: Effect of the vertical magnetic field to nonlinear Rayleigh-Taylor instability with an upper free surface.
Abstract: The magnetohydrodynamic analogue of the Rayleigh-Taylor (RT) instability arises when the fluids are electrically conducting and a magnetic field is present. We consider the incompressible magnetic RT instability in a horizontally slab domain being bounded above by a free surface and bounded below by a fixed bottom and show that the growth of the instability will be influenced by the vertical magnetic field.
Nguyễn Văn Thìn, Thai Nguyen University, Vietnam
Title: Normalized solutions and Qualitative properties of the solutions to wave equation involving fractional laplacian
Abstract: This talk contains two parts:
In the first part, I present some recently results about normalized solution to Elliptic equations.
In the second part, I will talk about some qualitative analysis of solutions to the Cauchy problem of wave equations involving the fractional Laplace operator with critical exponential nonlinearity. By using the contraction mapping principle, we show that the above Cauchy problem has a unique local solution. With the help of the potential well argument, we characterize the stable sets by the asymptotic behavior of solutions as t goes to infinity, as well as the unstable sets by the blow-up of solutions in finite time. Next, we investigate the finite-time blow-up of weak solutions to a class of wave equations involving the fractional Laplace operator with critical exponential growth, where the initial energy is
supercritical. Our results are published in [1], [2] and [3].
References
[1] Claudianor O. Alves and Nguyen Van Thin, On existence of multiple normalized solutions to a class of elliptic problems in whole R^N via Lusternik-Schnirelman category, SIAM Journal on Mathematical Analysis. 55(2), 1264-1283, 2023.
[2] Tahir Boudjeriou and Nguyen Van Thin, Asymptotics for a wave equation with critical exponential nonlinearity, Nonlinear Analysis: Real World Applications. Volume 78, August 2024, Article number:104099.
[3] Tahir Boudjeriou, Ngo Tran Vu and Nguyen Van Thin, High Energy Blowup for a Class of Wave Equations with Critical Exponential Nonlinearity, Mathematical Methods in the Applied Sciences, 2025; 0:1–9, https://doi.org/10.1002/mma.10873.
