Summer school on Bayesian statistics and computation

1.  Schedule

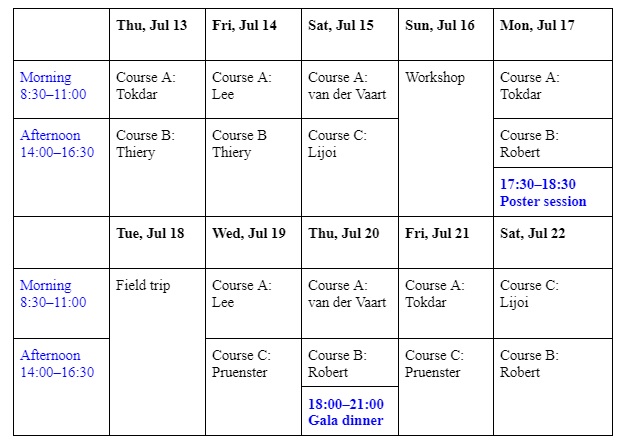
Lecture program consists of the following sequence, July 13—July 22, 2023

• Course A: Statistical and Bayesian foundations (Jaeyong Lee, Surya Tokdar,  and Aad van der Vaart).
• Course B: Bayesian computation (Christian Robert and Alex Thiery).
• Course C: Stochastic processes and Bayesian nonparametrics (Antonio Lijoi and Igor Pruenster).
• Teaching assistants: Đỗ Văn Cường, Đỗ Trọng Đạt, Sunrit Chakraborty.

There are 16 teaching modules, including 7 modules for Course A, 5 modules for Course B, 4 for Course C. Each module is 2.5 hours and will be taught in a morning or afternoon session.

Additional timeline

• July 13, 8—8:30 AM: Arrival/ Registration
• July 13, 8:30 AM: Opening Remark (VIASM/UEH/Organizer)
• July 13: Starts at 9 AM (all other dates start at 8:30 AM)
• Tea breaks: 9:30–10 in the morning, 3–3:30 in the afternoon
• Office hours: 11–11:30 in the morning with teaching assistants to go over lecture materials and homeworks

2 Course content

Surya Tokdar: Regression modeling, Bayesian applied modeling and inference 

• Lecture 1: “beginners”
• Lecture 2: “proficient”
• Lecture 3: “advanced”
• Reading materials: 
  • I will assume proficiency in probability theory and some familiarity with statistical methods, especially of the classical type. I won’t assume any in-depth training in Bayesian statistics, but a cursory introduction through any standard textbook (Hoff or DeGroot & Schervish) could be useful. As an alternative, I recommend a quick read of materials from my grad level inference course at Duke (STA 732 S14), especially the Bayesian content (starting from materials dated March 9th or later).
  • For applied Bayesian modeling, the most definitive book till date is Bayesian Data Analysis by Andrew Gelman and coauthors. This book could serve as excellent follow-up reading. 
  • A contrasting view is presented in the excellent modern statistics book by Brad Efron and Travor Hastie, titled Computer Age Statistical Inference. Some of my examples are taken from this book. Efron is not a Bayesian but has a deep appreciation for Bayesian thinking, especially when it comes to handling what he calls “indirect evidence” – a theme that pervades much of modern statistics and Efron’s own work on empirical Bayes. 

Jaeyong Lee: Basics of Bayesian inference, including testing and estimation

• Lecture 1
• Lecture 2
• Reading materials

Aad van der Vaart: Bayesian asymptotics, i.e., frequentist properties of Bayesian procedures, 

both parametric (BvM, coverage of credible sets) and nonparametric (consistency, rates, BvM, coverage, Dirichlet mixtures, Gaussian processes, inverse problems)

• Lecture 1
• Lecture 2
• Reading materials
  • Ghosal and van der Vaart, Fundamentals of Nonparametric Bayesian Inference, CUP 2017
  • Szabo and van der Vaart, Bayesian statistics, lectures notes available from  https://fa.ewi.tudelft.nl/~vaart/books/bayesianstatistics

Alex Thiery: Modern diffusion-based methods for sampling and inference. 

• Lecture 1
• Lecture 2

Reading: Working knowledge of the basics of diffusion processed.

Christian Robert: Methods in Bayesian computation

• Lecture 1: Monte Carlo principles
• Lecture 2: Markov Chain Monte Carlo methods (Gibbs, Metropolis-Hastings, HMC)
• Lecture 3: Approximate Bayesian Computation (ABC)
• While the course does not involve any practical and hence no requirement on coding or programming language, some background on algorithms will help. Similarly, a proficiency in probability theory and in particular Markov chain theory is expected, as well as some familiarity with statistical models since all examples are taken from Bayesian inference cases.
• Reading materials:
  • Monte Carlo Statistical Methods, C. Robert & G. Casella (2007) (basis of the first two lectures, see eg these slides), with a shorter version: Introducing Monte Carlo Methods with R (2009) [slides by George]
  • Monte Carlo theory, methods and examples, A. Owen (a different viewpoint with links to quasi Monte-Carlo as well)
  • Approximate Bayesian computation, a survey, C. Robert (2018)

Antonio Lịjoi and Igor Pruenster: Stochastic processes and Bayesian nonparametrics 

Contents

• Preliminaries and notation on the Bayes Laplace paradigm
• Merging of opinions
• Sequences of exchangeable random elements and de Finetti’s representation theorem
•  Random probability measures and existence theorem
• Dirichlet process: constructions and its main distributional properties
•  Predictive approach to Bayesian Nonparametrics and species sampling
• Gibbs-type priors and exchangeable random partitions
• Bayesian nonparametric models based on completely random measures
• More general forms of probabilistic symmetry: partial exchangeability
• Dependent processes
• Hierarchical processes: the hierarchical Dirichlet process and generalizations (hierarchical normalized random measures and Pitman-Yor processes)
•  Multivariate species sampling models

• Reading materials

• Camerlenghi, F., Lijoi, A., Orbanz, P. and Prünster, I. (2019). Distribution theory for hierarchical processes. The Annals of Statistics, 47, 67-92.
• De Blasi, P., Favaro, S., Lijoi, A., Mena, R., Prünster, I. and Ruggiero, M. (2015). Are Gibbs-type priors the most natural generalization of the Dirichlet process? IEEE Transactions on Pattern Analysis and Machine Intelligence, 37, 212-229
• Ghosal, S. and van der Vaart, A. (2017). Fundamentals of Nonparametric Bayesian Inference. Cambridge University Press.
• Lijoi, A. and Prünster, I. (2010). Models beyond the Dirichlet process. In Bayesian Nonparametrics (Hjort, N.L., Holmes, C.C., Müller, P., Walker, S.G. Eds.), Cambridge University Press, 80-136.
• Kingman, J.F.C. (1993). Poisson Processes. Oxford University Press