Hội nghị Lý thuyết Số Châu Á 2024 (PANT 2024) được tổ chức trong vòng 1 tuần, từ 15 đến 19 tháng 7 tại Viện Nghiên cứu cao cấp về Toán. Hội nghị PANT được khởi xướng bởi Giáo sư John Coates và một nhóm các Nhà khoa học thuộc lĩnh vực Lý thuyết số có uy tín ở Châu Á hoặc có nguồn gốc Châu Á. Mục tiêu của hội nghị là nhằm khuyến khích việc nghiên cứu Lý thuyết số ở khu vực Châu Á, đặc biệt thúc đẩy sự hợp tác giữa các nhà nghiên cứu trẻ về Lý thuyết số trong khu vực. Trong những năm gần đây Hội thảo lần lượt được tổ chức tại Hàn Quốc (2009, 2014), Nhật Bản (2010, 2021), Trung Quốc (2011, 2015, 2023), Ấn Độ (2012), Việt Nam (2013), Đài Loan (2016), Singapore (2018). Đây là lần thứ hai Việt Nam đóng vai trò chủ nhà của PANT.

Ban Chương trình PANT với sự tham gia của nhiều nhà khoa học nổi tiếng như GS.Akshay Venkatesh (Đại học Stanford và Viện Nghiên cứu cao cấp, Mỹ) - Huy chương Fields 2018; GS.Youngju Choie (Đại học Khoa học và Công nghệ Pohang, Hàn Quốc) - thành viên Hiệp hội Toán học Hoa Kỳ; GS.Ngô Bảo Châu (Đại học Chicago, Mỹ và VIASM, Việt Nam); GS. Wee Teck Gan (Đại học Quốc gia Singapore); GS.Mahesh Kakde (Viện Khoa học Ấn Độ) - Báo cáo mời Đại hội Toán học thế giới năm 2022,…

PANT 2024 với sự tham gia của 23 báo cáo mời đến từ 10 quốc gia: Việt Nam, Singapore, Đài Loan, Trung Quốc, Hàn Quốc, Nhật Bản, Ấn Độ, Anh, Pháp và Mỹ. Các báo cáo mời của PANT 2024 tập trung vào nhiều vấn đề thời sự của Lý thuyết số, bao gồm nhiều chuyên đề mang tính kết nối và bổ trợ lẫn nhau. Các chuyên đề bao gồm chương trình Langlands, chương trình Langlands phạm trù, các biểu diễn Galois, các dạng modular, các hàm zeta và hàm L cổ điển và hiện đại, các giá trị zeta bội, … cùng các liên hệ tới các lĩnh vực khác như Hình học số học, Lý thuyết biểu diễn.

Báo cáo mời toàn thể của GS. Mahesh Kakde - thành viên Ban Chương trình PANT đã giới thiệu về giả thuyết số Tamagawa đẳng biến (equivariant) liên hệ hạng tử dẫn đầu của L-hàm của một motive với các bất biến số học của motive đó, đồng thời cũng trình bày các kết quả mà nhóm nghiên cứu của Giáo sư đã đạt được liên quan đến giả thuyết này.

Một số nội dung chi tiết về các báo cáo mời khác như sau:

• GS. Ngô Đắc Tuấn giới thiệu về giả thuyết Hoffmann-Zagier, về tính chất đại số của các giá trị hàm zeta bội, và trình bày các kết quả mà nhóm nghiên cứu của GS đạt được về tương tự của giả thuyết này khi thay vành số nguyên bằng vành đa thức một biến trên trường hữu hạn.
• PGS. Sungyoon Cho trình bày nghiên cứu của mình về tổng quát hóa của giả thuyết Kudla-Rapoport liên hệ các mật độ biểu diễn với các chỉ số giao của các chu trình đặc biệt trong các trường hợp ở cấp độ parahoric.
• GS. Yihang Zhu trình bày các kết của nghiên cứu của mình và các cộng sự về mô tả đối đồng điều l-adic của các đa tạp Shimura gắn với các nhóm unita được phỏng đoán bởi Langlands.
• PGS. Jingren Chi trình bày nghiên cứu của mình về các vấn đề liên quan đến tích phân quỹ đạo xuất hiện trong phương pháp đếm điểm Langlands-Kottwitz.
• PGS. Ashay Burungale trình bày các kết quả của nhóm nghiên cứu về tính không triệt tiêu mod p của các giá trị đặc biệt của L-hàm Hecke trên các trường bậc hai ảo.
• GS. Bùi Mạnh Hùng trình bày các nghiên cứu của mình và cộng sự về bài toán moment bậc âm của hàm zeta Riemann.
• TS. Nguyễn Kiều Hiếu trình bày về kết quả của bản thân tính tường minh tác động phổ của Fargues-Scholze cho một lớp lớn các trường hợp cho nhóm GL_n.
• PGS. Lê Hùng Việt Bảo trình bày về các tính toán của đối đồng điều của đại số Hecke phổ xuất hiện trong chương trình Langlands phạm trù p-adic.
• PGS. Chan Ho Kim trình bày cách tiếp cận mới của mình về việc sử dụng các hệ Euler để chứng minh tính tự đẳng cấu của các biểu diễn Galois, vốn là cách tiếp cận ban đầu bị lỗi của Wiles trong lời giải bài toán Fermat.
• TS. Hiroki Kato trình bày một cách tiếp cận tổng quát về tình không phụ thuộc l của các nhóm đối đồng điều l-adic cho các đa tạp đại số/giải tích p-adic thông qua lý thuyết các chu trình cận kề motivic.
• TS. Zhilin Luo trình bày về các kết quả gần đây đạt được cùng GS. Ngô Bảo Châu về hạch của biến đổi Fourier tổng quát trong chương trình Braverman-Kazhdan cho nhóm SL_2 và GL_2.

Sau 5 ngày làm việc tích cực và sôi nổi, hội thảo PANT 2024 đã tạo cơ hội tuyệt vời cho các nhà nghiên cứu tại Việt Nam được tiếp cận với những kết quả nghiên cứu mới nhất trong lĩnh vực Lý thuyết số; đồng thời thúc đẩy nhiều cơ hội hợp tác trong tương lai với các nhà nghiên cứu tại khu vực châu Á nói riêng và trên thế giới nói chung.

Dưới đây là một số hình ảnh tiêu biểu tại Hội nghị: 07.15-19.2024. PANT2024

Các báo cáo mời và đại biểu tham dự PANT2024

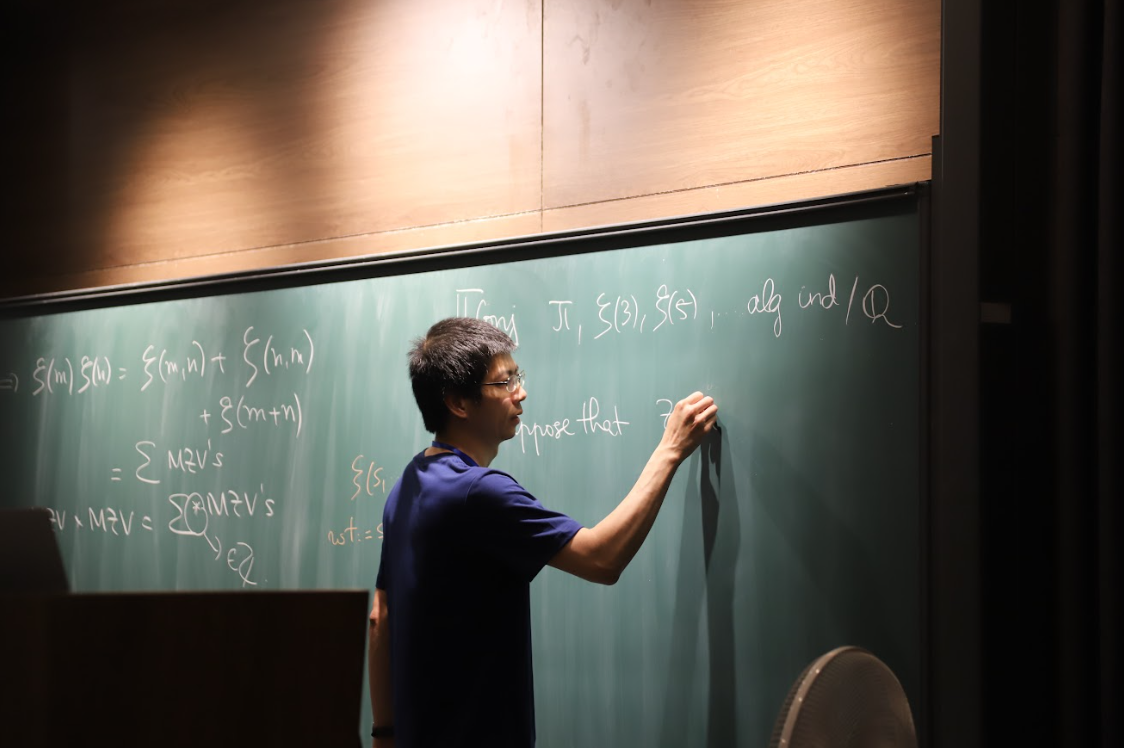
GS. Ngô Đắc Tuấn trình bày báo cáo khai mạc “On alternating multiple zeta values in positive characteristic”

GS. Ngô Bảo Châu chủ trì một phiên báo cáo tại Hội nghị

GS. Mahesh Kakde trình bày báo cáo “Refinements of the Brumer–Stark conjecture and ETNC”

GS. Bùi Mạnh Hùng trình bày báo cáo “Negative moments of the Riemann zeta-function”

TS. Chien-Hua Chen trình bày báo cáo “On singular moduli for higher rank Drinfeld modules”

Đại biểu tham dự Hội nghị

Tiệc chào mừng Hội nghị tại Căng tin Viện Nghiên cứu cao cấp về Toán

Trong giờ giải lao