Tại đại hội toán học thế giới 2018 được tổ chức tại Brasil, Bốn nhà toán học được Huy chương Fields năm 2018.
Danh sách gồm có:
1. Peter Scholze, 30 tuổi, Giáo sư đại học Bonn, Đức. (GS. Peter Scholze từng được Huy chương vàng tại IMO 2007 ở Hà Nội).
2. Alessio Figalli, 34 tuổi, người Ý, hiện đang làm việc tại ETH Zurich.
3. Akshay Venkatesh, 36 tuổi, Người Úc, hiện đang làm việc tại Institute of Advanced Study, Princeton, Hoa kỳ.
4. Caucher Birkar, 40 tuổi, người gốc Kurd thuộc Iran, hiện đang làm việc tại Đại học Cambridge, Anh quốc.
------------------------------
Huy chương Fields 2018: Peter Scholze
Peter Scholze vừa được trao tặng huy chương Fields, tại Đại hội Toán học Thế giới tại Rio de Janeiro (Brazil), "vì những đóng góp làm thay đổi hình học đại số số học trên các trường p-adic thông qua việc giới thiệu các không gian perfectoid, với ứng dụng vào biểu diễn Galois, và vì sự phát triển của các lý thuyết đối đồng điều mới".

Không gian perfectoid là minh chứng cho sự sống động của toán học, chỉ mới được Scholze giới thiệu năm 2011 (khi anh 23 tuổi). Mặc dù là một thứ toán học mới, khái niệm không gian perfectoid giúp Scholze và các đồng nghiệp chứng minh thành công những bài toán mở quan trọng trong hình học đại số và nhiều lĩnh vực khác. Công việc của anh đã gắn kết các lĩnh vực của toán học bao gồm tôpô học (nghiên cứu hình dạng của các vật thể toán học), lý thuyết Galois (áp dụng tính đối xứng vào nghiên cứu các nghiệm của các phương trình) và hình học p- adic (mà chúng tôi sẽ mô tả dưới đây).
Cảm hứng để sinh ra các không gian perfectoid bắt nguồn từ việc Scholze đi tìm câu trả lời cho các câu hỏi về các phương trình trên các trường nền khác nhau. Trường là khái niệm mở rộng từ các số thực và số hữu tỷ mà chúng ta đã gặp trong đại số. Nó là một tập hợp các số với các phép toán số học trên đó được thực hiện đúng như cách mà phép cộng, phép trừ, phép nhân và phép chia thực hiện cho các số hữu tỷ và các số thực. Chẳng hạn, tập hợp bảy số 0, 1, …, 6 với các phép toán số học đồng dư modulo 7 là một trường:
Trong ví dụ này, số 0 tác động giống như số 0 mà chúng ta thường sử dụng – nó là phần tử trung lập đối với phép cộng . Số 1 trong trường này giống như số 1 chúng ta quen dùng: nó là phần tử trung lập đối với phép nhân
. Nhưng có một điều khác biệt xảy ra trong trường này khi ta cộng liên tiếp với số 1, bảy lần :
Cộng các số 1 với nhau trong trường các số thực hoặc trường các số hữu tỷ không bao giờ có kết quả bằng 0. Sự khác nhau bắt nguồn bởi đặc số của trường - trường đồng dư modulo 7 có đặc số bằng 7. (Với một trường bất kì xác định bởi đồng dư modulo một số nguyên tố p, đặc số của nó chính là p.) Vì không thể thực hiện được điều này đối với các số thực hoặc các số hữu tỷ, cả hai trường số thực và số hữu tỷ đều có đặc số 0.
Scholze đã làm việc với các bài toán liên quan đến các trường khác nhau, đôi khi những bài toán này liên quan đến cả trường có đặc số p (với p là một số nguyên tố) và trường có đặc số 0 cùng “họ” với nó. Đặc biệt, Scholze muốn giải các bài toán trong các trường số học p-adic, những trường này có đặc số 0. Trong các trường vô hạn như thế này, số p biểu thị một số nguyên tố đo độ gần nhau của hai số theo một cách mới (chẳng hạn, 2-adic, 3-adic, 5-adic, vân vân). Đối với cách đo độ gần nhau này, hai số gần nhau không có nghĩa chúng có giá trị gần nhau, mà là hiệu của chúng chia hết cho một lũy thừa của số nguyên tố p. Lũy thừa đó càng cao thì hai số đó càng gần nhau.
Ví dụ, trong số học, chúng ta đã biết các số 3 và 67 không gần nhau lắm, nhưng nếu so với 3 và 1027 thì chúng gần nhau hơn. Tuy nhiên, trong số học 2-adic, 3 và 1027 khác nhau 2^10 , 3 và 67 khác nhau chỉ 2^6 , do đó 3 và 1027 gần nhau hơn 3 và 67.
Khái niệm mới về độ gần nhau của các cặp số dường như là một khái niệm kì quặc, nhưng số học p-adic rất hữu dụng trong các lĩnh vực như Lý thuyết số khi ta muốn giải các phương trình đồng dư modulo một lũy thừa của một số nguyên tố p.
Đôi khi, giải quyết các bài toán trên trường đặc số nguyên tố dễ dàng hơn trên trường đặc số 0. Do đó, Scholze đã đề xuất khái niệm “perfectoid” như một cách để “dịch chuyển” các trường đặc số 0 thành các trường đặc số p. Phương pháp này phức tạp và không gian perfectoid được tạo ra là một vật thể giống fractal, uốn khúc vô hạn, là cầu nối số học p-adic và hình học. Các không gian perfectoid là các không gian mà trong đó số học p-adic có thể được sử dụng để hiểu hình học và tôpô của các không gian, kết nối các lĩnh vực khác nhau của toán học và cho phép các công cụ từ lĩnh vực này được sử dụng trong lĩnh vực khác.
Không gian perfectoid tác động lớn đến toán học chỉ sau một khoảng thời gian rất ngắn: một lĩnh vực nghiên cứu mới đang lớn mạnh, giải quyết những bài toán mở và mở ra những hướng đi mới cho nghiên cứu. Khái niệm này thậm chí có thể tỏa sáng trên một số khía cạnh sâu sắc hơn và mang ý nghĩa thống nhất toán học.

Thành công của Scholze cũng giúp chúng ta thấy rõ vai trò của toán học như một ngôn ngữ, và tầm quan trọng của việc có một ngôn ngữ thích hợp cho công việc mà chúng ta đang cố gắng thực hiện. Scholze phát biểu: “Vấn đề mấu chốt đối với tôi là tìm thấy các định nghĩa đúng, các khái niệm đúng, những thứ thực sự cắt nghĩa được bản chất của một số hiện tượng toán học.
Tôi thường mơ hồ nhìn thấy những điều mà tôi muốn hiểu nhưng tôi thường không đủ ngôn từ để diễn đạt chúng. Nhưng đôi khi tôi đọc được một bài báo trình bày định nghĩa về chúng, tôi bất chợt nhận ra có thể nói được ra những điều tôi muốn nói.” Scholze đang mở rộng ngôn ngữ toán học, giúp chúng ta kể những câu chuyện toán học mới mẻ, đẹp đẽ và có thể làm chúng ta bất ngờ.
(nguồn: https://plus.maths.org/content/ps, người dịch: Lê Quý Thường, Đỗ Việt Cường)
-----------------------------------------
Huy chương Fields 2018: Alessio Figalli
(Tác giả: Marianne Freiberger)
Alessio Figalli vừa được trao giải thưởng Fields vì "những đóng góp của ông cho lý thuyết vận tải tối ưu và ứng dụng của nó vào phương trình đạo hàm riêng, hình học metric và xác suất."
 Ảnh được chụp bởi Tatjana Ruf.
Ảnh được chụp bởi Tatjana Ruf.
Đây là một danh sách dài những thuật ngữ toán học khó nuốt. Do vậy hãy chỉ tập trung vào hai từ mà có lẽ tất cả chúng ta đều hiểu: "vận tải" và "tối ưu". Cái tên đã nói lên tất cả. Lý thuyết vận tải tối ưu nghiên cứu về việc tìm ra phương án tốt nhất, ứng với mỗi một yêu cầu cụ thể, để thực hiện việc phân phối, vận chuyển các đồ vật (hàng hóa,…) từ nơi này đến nơi khác.
Hãy xét một ví dụ đơn giản. Tưởng tượng rằng bạn có một chuỗi các mỏ vàng và muốn vận chuyển lượng vàng khai thác được từ mỗi mỏ về một ngân hàng để lưu giữ. Giả sử số lượng các ngân hàng và số lượng các mỏ vàng là như nhau. Nhiệm vụ của bạn là quyết định xem vàng của mỏ nào nên được chuyển vào ngân hàng nào.
Cách tối ưu để làm việc này phụ thuộc vào nhu cầu của bạn. Nếu bạn đơn giản chỉ muốn giảm thiểu tổng quãng đường vận chuyển thì bạn cần chọn tương ứng cho mỗi mỏ vàng một ngân hàng nào đó sao cho tổng các khoảng cách từ các mỏ vàng đến các ngân hàng tương ứng là nhỏ nhất có thể. Nhưng bất cứ ai đã dùng hệ thống định vị vệ tinh đều biết rằng đường ngắn nhất chưa chắc đã nhanh nhất. Vì thế, nếu bạn muốn làm giảm thiểu tổng thời gian vận chuyển thì bạn có thể cần thay đổi cách ghép cặp ngân hàng-mỏ vàng của bạn.
Tổng quát hơn, bạn có một hàm chi phí c(x,y) cho bạn biết chi phí vận chuyển (được tính theo khoảng cách, thời gian, hay một yếu tố nào khác,....) ứng với mỗi cặp mỏ x và ngân hàng y. Và bạn muốn tìm một cách ghép cặp mỏ vàng-ngân hàng sao cho tổng các hàm chi phí của tất cả các cặp là nhỏ nhất có thể.
Từ thuở sơ khai, con người đã phải đối mặt với bài toán vận tải tối ưu, dưới dạng này hay dạng khác. Tuy nhiên, chúng chỉ mới được nghiên cứu một cách toán học vào cuối thế kỉ XVIII bởi một kĩ sư người Pháp tên là Gaspard Monge - người đã quan tâm đến câu hỏi tìm cách tốt nhất xúc cát từ một đống cát để lấp đầy một hố có cùng thể tích. Monge đã không nghĩ về các đồ vật (hàng hóa) được đặt ở các vị trí rời rạc, ví dụ như các mỏ vàng của chúng ta như ở trên, mà chúng được phân bố liên tục giống như các hạt cát. Vì thế, đại lượng mà chúng ta cần tối ưu không phải là một tổng hữu hạn mà là một tích phân ứng với các độ đo cụ thể - những ai đã quen thuộc với những khái niệm này có thể tìm thấy công thức chính xác của hàm vận tải tối ưu Monge đường dẫn sau:
https://en.wikipedia.org/wiki/Transportation_theory_(mathematics)#Monge_and_Kantorovich_formulations
Với vấn đề được đặt ra như trên, bài toán vận tải tối ưu đã chuyển từ cái mà chúng ta có thể giải được tương đối dễ dàng bằng giấy và bút chì thành một vấn đề sâu sắc trong lý thuyết các hàm toán học. Trên thực tế, với cách thiết lập này, bài toán Monge không phải lúc nào cũng giải được vì hàm vận tải tối ưu phù hợp có thể không tồn tại. Phải đến những năm 1940, Leonid Kantorovich mới đưa ra một phát biểu lại vô cùng khéo léo cho bài toán và làm nó trở nên dễ tiếp cận hơn (mặc dù các nghiệm của bài toán Kantorovich không phải lúc nào cũng chuyển được thành các nghiệm của bài toán Monge).
Về mặt toán học, có nhiều hướng để chúng ta có thể tiếp cận với một bài toán vận tải tối ưu tổng quát. Ví dụ như, chúng ta có thể xét nhiều hàm chi phí khác nhau và xét xem liệu một nghiệm tối ưu có tồn tại cho một trong những hàm chi phí đó hay không và nếu có thì làm thế nào để tìm được nó. Chúng ta cũng có thể thay đổi không gian nền: ở trên chúng ta đã giả thiết rằng các mỏ vàng và các đống cát tồn tại trong không gian Euclid thông thường, nhưng nếu những thứ mà chúng ta muốn di chuyển tồn tại trong một không gian hình học kì lạ hơn thì sao? Một khi có nghiệm tối ưu, bạn cũng có thể muốn tự hỏi bản thân rằng nó có những tính chất toán học gì, nghiệm này có tốt theo một nghĩa nào đó (trơn chẳng hạn) hay phức tạp hơn?
Alessio Figalli đã được vinh danh cho những nghiên cứu của mình đối với những câu hỏi như vậy. Và nếu bạn quen thuộc với lĩnh vực toán học này, bạn có thể tìm thấy một danh sách đầy ấn tượng các công bố của Alessio Figalli về các vấn đề này tại đường dẫn sau:
https://people.math.ethz.ch/~afigalli/papers
Figalli còn được ngợi ca vì cách mà ông đã ứng dụng lý thuyết vận tải tối ưu vào các lĩnh vực toán học khác. Một ứng dụng vô cùng thú vị tác động rất lớn đến một vấn đề mà tất cả chúng ta phải đối mặt hàng ngày đó chính là thời tiết, hay chính xác hơn, dự báo thời tiết. "Để mô hình hóa các dòng không khí có kích cỡ lớn, các nhà khí tượng học dùng cái gọi là phương trình bán geostrophic", Figalli giải thích trong một video được sản xuất bởi Quĩ Simons. "Những phương trình này được dùng để dự đoán sự tiến triển của các đám mây." Nếu bạn nghĩ về đám mây như những chất điểm vô cùng bé di chuyển trong không gian thì việc hiểu được tất cả các chất điểm đã di chuyển như thế nào trong một khoảng thời gian liên quan đến việc giải một bài toán vận tải tối ưu. Chính sự kết nối này đã giúp Figalli và các cộng sự của ông có thể giải được những phương trình bán geostrophic này.
"Những năm gần đây, tôi đã xoay sở để giải một vài bài toán mà tôi muốn", Figalli nói trong cùng video nói trên. "Nhưng danh sách những việc tôi cần làm vẫn còn dài và tôi phải làm việc trong vòng hai ba mươi năm tới." Chúng ta chúc mừng Figalli đã giành được giải thưởng Fields danh giá và chúc ông mọi điều tốt đẹp nhất cho công việc trong tương lai. Đặc biệt, chúng ta hi vọng rằng ông sẽ sớm giải quyết được bài toán quan trọng với ông hơn bất cứ bài toán nào khác: xoay sở để được sống trong cùng một thành phố với một nhà toán học đặc biệt - vợ của ông.
Nguồn: https://plus.maths.org/content/test-2-0; Người dịch: Đoàn An Khương, Nguyễn Phụ Hoàng Lân. Phạm Văn Tuấn.
-----------------------------------------
Huy chương Fields 2018: Akshay Venkatesh
Akshay Venkatesh vừa được trao Huy chương Fields, tại Đại hội Toán học Thế giới 2018 tổ chức ở Rio de Jainero vì những đóng góp của ông trong việc “tổng hợp các lĩnh vực như Lý thuyết số giải tích, hệ động lực thuần nhất, tôpô, và Lý thuyết biểu diễn”.
Venkatesh nói ông luôn bị hấp dẫn bởi các số, từ việc khám phá ra các số nhị phân khi là một cậu bé, cho đến những công trình có tính đột phá của ông trong Lý thuyết số như một nhà toán học: ``Chỉ có việc điều khiển các số khiến tôi cảm thấy hạnh phúc". Lĩnh vực Lý thuyết số cũng lôi cuốn ông ta khi còn là một nhà toán học trẻ rằng bạn không cần quá nhiều kiến thức cơ sở để trân trọng các kết quả đẹp và các câu hỏi mở trong lĩnh vực này.
Hầu hết công việc của Venkatesh dành cho việc khám phá liên hệ giữa Lý thuyết số với các lĩnh vực toán học khác. Ông đã mang những khái niệm và công cụ từ các lĩnh vực khác nhau để tạo ảnh hưởng lớn đến việc giải quyết các vấn đề mở và chỉ ra con đường phát triển trong tương lai. Cách thức này được minh họa bằng lời giải của ông cho vấn đề lồi dưới (subconvexity) trong Lý thuyết số.
Vấn đề lồi dưới về cơ bản đề cập đến kích thước của một loại hàm cụ thể gọi là $L$-hàm. Các $L$-hàm là các khái quát của zeta-hàm Riemann, chủ đề của một vấn đề mở nổi tiếng trong Toán học được gọi là giả thuyết Riemann. (Bạn có thể đọc thêm về $L$-hàm ở https://plus.maths.org/content/one-l-discovery.) Vào thế kỷ 19, nhà Toán học Bernhard Riemann đã chỉ ra rằng các vị trí mà tại đó hàm zeta Riemann lấy giá trị bằng không được liên kết chặt chẽ với sự phân bố của các số nguyên tố (số chia hết cho 1 và chính nó) trong tập hợp các số. Điều này đã cách mạng hóa sự hiểu biết về các số nguyên tố trong thế kỷ 19 và giờ đây các $L$-hàm là các đối tượng then chốt trong Lý thuyết số hiện nay.
$L$-hàm là các hàm trên các số phức - những số dạng a+bi , trong đó a và b là số thực và i là căn bậc hai của -1 (i2 = -1). Giả thuyết Riemann, chưa được chứng minh, phỏng đoán rằng tất cả các vị trí mà hàm zeta Riemann triệt tiêu nằm dọc theo một cái gọi là đường thẳng tới hạn, trong đó phần thực của những số phức này bằng một nửa (tức là, ![]() ).
).
Vấn đề lồi dưới đề cập đến việc làm chặt chặn trên của độ lớn $L$-hàm dọc theo một đường thẳng tới hạn. Vấn đề này đã được quan tâm từ công trình của Herman Weyl cách đây một thế kỷ, nhưng đã được tập trung nghiên cứu mạnh mẽ hơn trong mươi, mười lăm năm trở lại đây vì các ứng dụng của nó, bao gồm liên hệ giữa Lý thuyết số và sự hỗn loạn trong các hệ lượng tử. Venkatesh, một phần cùng với Philippe Michel, đã giải quyết vấn đề lồi dưới vào năm 2010. Kết quả đã mở rộng tất cả các công việc trước đây về chặn của bài toán và cũng dùng các phương pháp tiếp cận từ Hình học Đại số, Hệ động lực và Lý thuyết số, trên con đường thu được chứng minh kết quả chính đã thu được chứng minh kết quả mới đáng chú ý trong các lĩnh vực này.
Venkatesh nói rằng ông hiểu các $L$-hàm bằng cách sử dụng hình học hyperbolic - một kiểu hình học đặc biệt. Bạn có thể lát một không gian hyperbolic với các hình tam giác nhưng, như bạn có thể thấy trong hình vẽ, hình tam giác hyperbolic có một chút khác biệt: tổng các góc của chúng nhỏ hơn 180 độ. Những phép lát hyperbolic này cung cấp một kết nối đáng ngạc nhiên giữa các lĩnh vực vực dường như khác nhau của Toán học.
Ví dụ, Venkatesh sử dụng các dạng tự đẳng cấu để nghiên cứu các phép lát hyperbolic này. Sóng âm được tạo ra từ việc chơi phần da phẳng trải dài trên trống có thể được mô tả bằng cách sử dụng các hàm tuần hoàn (sóng sin). Tương tự như các dạng tự đẳng cấu, phiên bản tổng quát của các hàm tuần hoàn, cho bạn biết kiểu âm của trống sẽ tạo ra nếu nó được xây dựng bằng cách sử dụng "da hyperbolic".
Các dạng tự đẳng cấu là một phần của một lĩnh vực toán học được có tên Giải tích điều hòa. Chúng được liên kết với Lý thuyết Hệ động lực (nghiên cứu về cách các vật di chuyển theo thời gian) bằng phép lát hyperbolic. Các kết nối động lực này có được từ phiên bản lý tưởng của việc chơi bi-a. Thay vì chơi trò bi-a trên bàn hình chữ nhật, bạn có thể tưởng tượng chơi trên một chiếc bàn có hình dạng như một viên gạch hyperbolic. Quỹ đạo của quả bóng nảy ra từ những mặt cong này rất phức tạp. Nghiên cứu những con đường bi-a di chuyển, cố gắng hiểu những miền bi-a tránh, hoặc bi-a bị hút, liên kết các câu hỏi Hình học và Động lực học với Lý thuyết số.
Và gần đây, Venkatesh đã làm việc trong một lĩnh vực gọi là đối đồng điều của các Nhóm số học, đề cập đến hình dạng hoặc tôpô của không gian sử dụng phép lát hyperbolic. Đây thực sự là những đối tượng nhiều chiều hơn với hình dạng phức tạp liên quan đến các lỗ. Và mặc dù xuất hiện lần đầu, có một liên hệ chặt chẽ giữa Lý thuyết số và các hình dạng chiều cao hơn này: "Rất nhiều thông tin về Lý thuyết số được mã hóa trong những hình dạng này."
Venkatesh đã rất thành công trong việc tạo ra các liên hệ đáng ngạc nhiên và phong phú giữa các lĩnh vực toán học khác nhau, nhưng ông ta không che giấu thực tế rằng việc thực hiện nó gặp rất nhiều khó khăn: "Rất nhiều thời gian khi làm Toán, bạn bị tắc. Nhưng cùng lúc đó có những khoảnh khắc mà bạn cảm thấy đặc quyền khi làm việc với nó. Và đó là một cảm giác tuyệt vời. Bạn cảm thấy như bạn đã là một phần của thứ gì đó thực sự có ý nghĩa.''
Nguồn: https://plus.maths.org/content/AV, người dịch: Đào Phương Bắc
-----------------------------------------
Huy chương Fields 2018: Caucher Birkar
Caucher Birkar, nhà toán học người Anh, gốc Iran, sinh năm 1978. vừa được vinh dự nhận giải thưởng Field 2018 do những đóng góp lớn của ông trong lĩnh vực hình học đại số. Như tên gọi, hình học đại số là lĩnh vực nghiên cứu các đối tượng hình học dựa trên các phương trình mô tả chúng.

Ở bậc trung học, ta đã được học và làm quen với các phương trình xuất hiện trong hình học phẳng và hình học không gian. Chẳng hạn, phương trình y=2x+1
mô tả một đường thẳng với độ dốc (hệ số góc) bằng 2 và cắt trục tung Oy tại điểm có toạ độ (0,1).
Tương tự, phương trình x2+y2=1.
mô tả một đường tròn có bán kính bằng 1 và tâm tại điểm (0, 0) (theo Định lý Pythagoras, xem hình bên dưới).
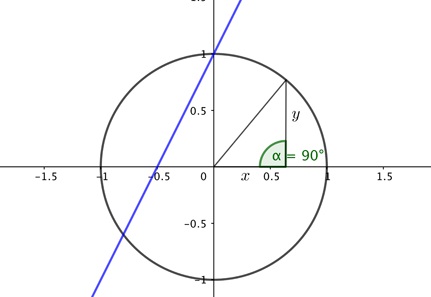
Hình. Đường thẳng màu xanh có phương trình y=2x+1 và đường tròn đơn vị có phương trình x2+y2=1.
Đường tròn và đường thẳng là những ví dụ về đường cong đại số (algebraic curves) trên mặt phẳng Euclid: những đường cong được định nghĩa bằng phương trình đại số.
Tăng lên một chiều, ta cũng có thể xét các mặt đại số (algebraic surfaces). Mặt cầu trong không gian Euclid ba chiều có tâm tại điểm (0,0,0) và bán kính 1 là một ví dụ. Tương tự với đường tròn trong không gian hai chiều, mặt cầu được mô tả bởi phương trình đại số
x2+y2+z2=1
Và như ta có thể hình dung, một mặt phẳng trong không gian ba chiều là một ví dụ khác về mặt đại số.
Không dừng lại đó, các phương trình đa thức phức tạp hơn, trên các trường số khác nhau (ví dụ như trường số phức), sẽ dẫn đến khái niệm tổng quát về một đa tạp đại số (algebraic variety). Đường cong và mặt phẳng đại số là những về dụ về các đa tạp đại số, nhưng những đa tạp đại số tổng quát có thể phức tạp hơn: chúng có thể tồn tại trong các không gian có chiều cao hơn mà ta không thể hình dung trực quan được. Tuy nhiên, điều đó cũng không cản trở các nhà toán học, bởi vì từ lâu họ đã phát triển một phương pháp nghiên cứu hình học trong trường hợp nhiều chiều.
Khi được cho trước một tập (zoo) vô hạn các đa tạp đại số, người ta tìm cách phân loại chúng thành các họ (families), cũng giống như cách người ta phân loại trong một bộ sưu tập các loài bướm. Trở lại ví dụ đơn giản phía trên, ta có thể mong muốn phân loại chúng theo hình dạng: phân các đa tạp đại số giống như các mặt phẳng vào một họ, phân các đa tạp đại số giống như các khối cầu vào một họ khác, v.v…
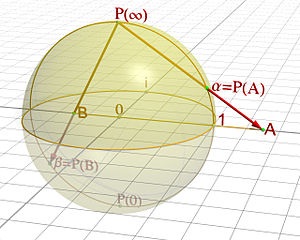

Phép chiếu mà chúng ta vừa xem xét là một ví dụ của một ánh xạ song hữu tỉ (birational map). Các ánh xạ song hữu tỉ được định nghĩa trong bối cảnh tổng quát hơn và được sử dụng để biến đổi các đa tạp đại số phức tạp hơn so với các mặt cầu hay mặt phẳng. Có nhiều lí do hợp lý cho việc tại sao chúng ta có thể biến đổi chúng theo cách này. Một trong những lý do đó là việc không phải mọi đa tạp đại số đều đẹp và trơn (smooth) như các mặt phẳng hay mặt cầu mà chúng ta vừa nói trên. Một số đa tạp đại số chứa những điểm kì dị (singular points) (như các điểm nhọn (cusps) chẳng hạn) khiến việc xử lý chúng khó khăn. Ít nhất khi ta gặp một loại đa tạp đại số cụ thể nào đó (trên trường có đặc số 0), tính linh động của các ánh xạ song hữu tỉ cho phép chúng ta biến đổi một đa tạp “xấu xí” (do chứa điểm kì dị) trở thành một đa tạp xạ ảnh trơn (smooth projective variety) không chứa điểm kì dị. Như vậy, trong trường hợp đó, thậm chí khi gặp một đa tạp đại số xấu xí, phức tạp, khó xử lý, ít nhất chúng ta cũng biết được một đa tạp đại số đẹp hơn có mối quan hệ song hữu tỉ với nó. Do đó, theo một nghĩa nào đó, các đa tạp có mối quan hệ song hữu tỉ với nhau có thể được xem như cùng vào một họ.
Birkar làm việc trong lĩnh vực hình học song hữu tỉ (birational geometry), lĩnh vực nghiên cứu việc phân loại các đa tạp đại số theo cách trên. Đặc biệt, các nhà toán học hy vọng có thể chứng minh được rằng mọi đa tạp đại số đều có quan hệ song hữu tỉ một loại đa tạp đại số đẹp một cách đặc biệt được tạo thành từ “ba khối xây dựng cơ bản” (three basic building blocks). Việc chứng minh được giả thuyết này liên quan đến việc giải quyết một số bài toán lớn, đó là giả thuyết minimal model và giả thuyết abundance. Trong lĩnh vực này, Birkar đã có những đột phá lớn, và ông được trao Huy chương Fields cho …
“... chứng minh của ông về tính bị chặn của các đa tạp Fano và cho những đóng góp của ông trong ‘chương trình mô hình tối thiểu’ (minimal model program).
Birkar sinh năm 1978 trong một gia đình nông dân ở Tỉnh Kurdistan của Iran, và đi học phổ thông trong sự hỗn loạn của cuộc chiến tranh Iran-Iraq. “Là chiến trường, Kurdistan không phải là một nơi để cho một cậu bé phát triển mối quan tâm đến toán học”, Birkar đã nói như thế trong trong video chấp nhận của mình được chiếu tại lễ khai mạc ICM ở Rio de Janeiro. Chính anh trai của ông đã dạy cho ông những kiến thức toán cấp cao mà ông chưa được học ở trường, và cuối cùng ông đã học toán tại Đại học Tehran. Năm 2000, ông chuyển đến Anh, nơi ông đã được cấp quy chế tị nạn và hoàn thành bằng tiến sĩ. Ông hiện là Giáo sư tại Khoa Toán - Thống kê của Đại học Cambridge.
(Nguồn: Marianne Freiberger, https://plus.maths.org/content/test-1-0) ; Người dịch: Tăng Khải Hạnh, Đoàn An Khương
