Tiếp theo thành công của trường hè VIASM-ICTP năm 2022 về lý thuyết biểu diễn và lý thuyết nhóm, hè năm 2023, từ ngày 14 đến 25 tháng 8, Viện Nghiên cứu cao cấp về Toán (VIASM) phối hợp với Trung tâm Quốc tế về Vật lý lý thuyết (ICTP) tiếp tục tổ chức Trường hè về chủ đề Hình học vi phân. Năm 2023, Viện toán học Clay (Clay Math Institute) tiếp tục đồng hành cùng Viện NCCCT và ICTP. Bên cạnh đó, trường cũng nhận được sự tài trợ của CNRS (Pháp) và Hội toán học thế giới (IMU).
Tham gia sự kiện có hơn 70 nhà khoa học và các bạn học viên thuộc lĩnh vực Giải tích, Hình học, Tôpô, của các Trường, Viện trong và ngoài nước tham gia. Bên cạnh các đại biểu trong nước, Trường hè còn chào đón hơn 30 nhà khoa học và học viên đến từ nhiều quốc gia trên thế giới bao gồm Trung Quốc, Ấn Độ, Nhật Bản, Hàn Quốc, Philippine, Australia, Italia, Tây Ban Nha, Ba Lan, Cộng hòa Séc, Pháp, và Mỹ. Đặc biệt, trong số các đại biểu nước ngoài có rất nhiều nhà toán học nổi tiếng trên thế giới như là GS. Andre Neves (Đại học Chicago, Hoa kỳ), GS. Jean Pierre Bourguinon (IHES, Cộng hoà Pháp), và GS Richard Schoen (UCI, Hoa Kỳ).

GS.TSKH. Ngô Bảo Châu, Giám đốc khoa học VIASM phát biểu khai mạc Trường hè

Phát biểu khai mạc Trường hè, GS. Ngô Bảo Châu, Giám đốc khoa học VIASM nhấn mạnh tầm quan trọng của Hình học vi phân trong sự phát triển của Toán học đương đại với nhiều tiềm năng ứng dụng và các thành tựu đột phá. Giáo sư cũng khẳng định sự cần thiết trong việc giao lưu, hợp tác nghiên cứu và phát triển cộng đồng nghiên cứu ở Việt Nam. Với mục tiêu hướng tới sự phát triển bền vững và xây dựng được một đội ngũ các nhà nghiên cứu có chuyên môn cao về hình học giải tích và các lĩnh vực liên quan, Trường Hè 2023 sẽ đóng góp một phần quan trọng vào việc thúc đẩy sự phát triển của cộng đồng nghiên cứu Toán học và Khoa học nói chung. Trường hè cũng là cầu nối giữa các thế hệ trẻ Việt Nam và khu vực trong việc tiếp cận các hướng nghiên cứu hiện đại, kết nối với các chuyên gia hàng đầu trong lĩnh vực.

Giảng viên, Ban tổ chức và Học viên của Trường hè chụp ảnh sau buổi Khai mạc

Trường hè đã diễn ra trong 2 tuần với các hoạt động giảng dạy, hội thảo khoa học giữa các nhà khoa học hàng đầu trong lĩnh vực Hình học vi phân trên thế giới GS. J. P. Bourguinon (IHES, Pháp), GS. R. Schoen (UCI, Mỹ), GS. C. Arrezo (ICTP, Italia), GS. C. Sormani (CUNY Mỹ), GS. G. F. Wei (UCSB, Mỹ), GS. S. Ohta (Osaka, Nhật), GS. A. Pulemotov (Queensland, Úc), GS. A. Neves (Chicago, Mỹ)... Trong đó, đặc biệt GS. R. Schoen có ba lần báo cáo mời Hội nghị toán học thế giới; GS. Bourguinon (Giám đốc viện nghiên cứu cao cấp IHES của Pháp, chủ tịch Hội đồng nghiên cứu Châu u), GS. C. Azzerro (Trưởng phân viện toán, ICTP), GS. A. Neves là chuyên gia hàng đầu thế giới, người đã cũng với F. Marques đưa ra lời giải cho Giả thuyết Willmore.
Trường hè còn có trợ giảng là các nhà Toán học trẻ trong nước trong lĩnh vực này là PGS. Nguyễn Thạc Dũng và TS. Nguyễn Minh Hoàng; đặc biệt PGS. Trần Thanh Hưng (Texas, Mỹ) cũng cùng tham gia các công việc tổ chức. Trong các phản hồi của GS. A. Pulemotov, GS. S. Ohta về lần đầu đến với Việt Nam, các nhà toán học này đều nhấn mạnh họ rất thích thú tham gia trường hè và các hoạt động liên quan. Các nhà toán học hứa nhất định sẽ trở lại Việt Nam.

GS. B. Allen giảng chuyên đề “Convergence of Riemannian Manifolds and Scalar Curvature”

GS. A. Neves giảng chuyên đề “Minimal surfaces and Zoll metrics ”

GS. C. Arrezo giảng chuyên đề “The geometry of constant scalar curvature Kahler manifolds”

GS. A. Pulemotov giảng chuyên đề “The prescribed Ricci curvature problem”

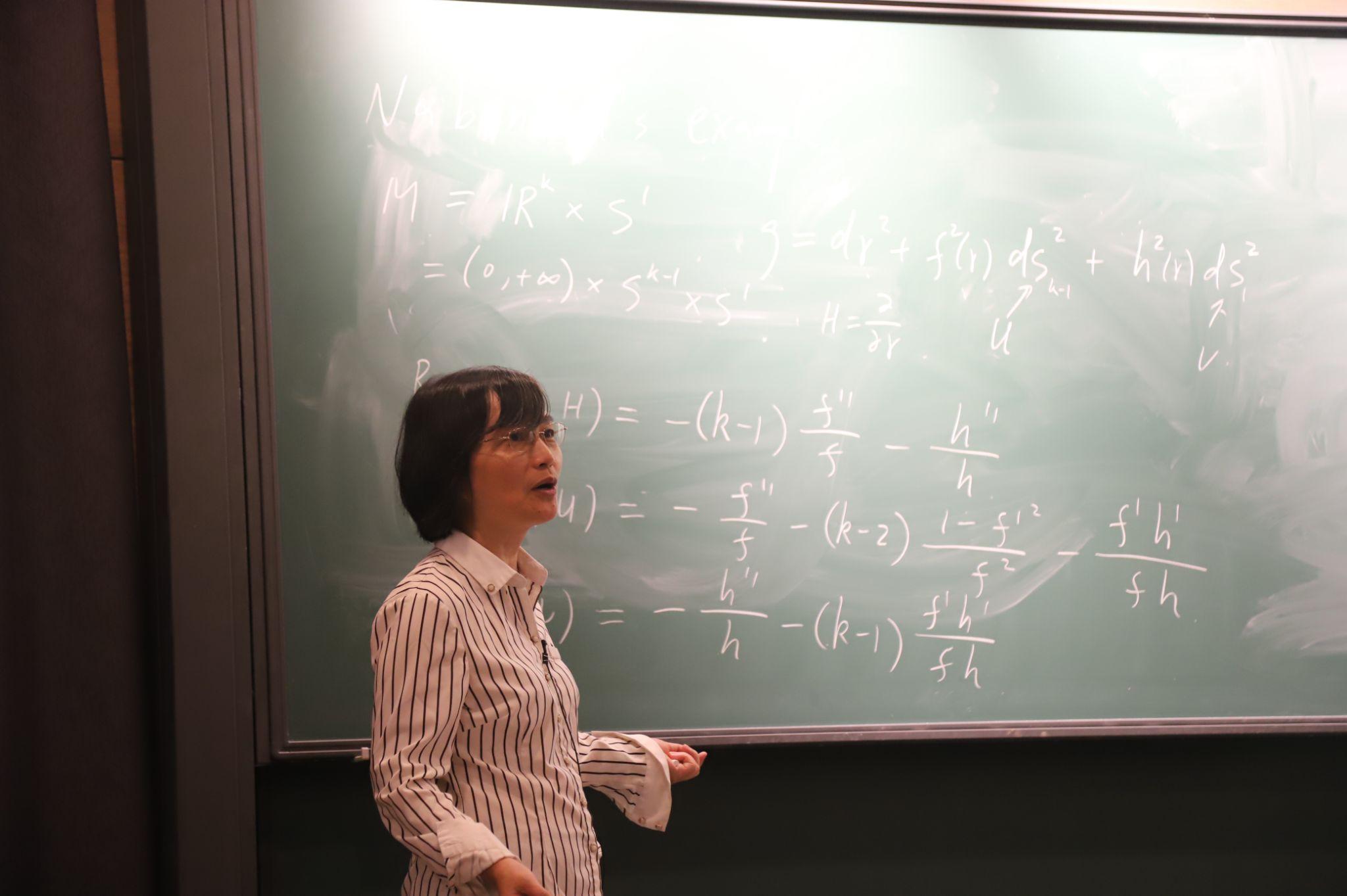
GS. G.F. Wei giảng chuyên đề “Some recent results for spaces with Ricci curvature lower bounds”

Các bài giảng của trường hè tập trung vào nhiều vấn đề thời sự của toán học đương đại bao gồm: Hình học hội tụ của các đa tạp Riemann và độ cong vô hướng, Bài toán độ cong Ricci mô tả trước, Các mặt cực tiểu và metric Zoll, hình học của các đa tạp Kahler với độ cong vô hướng không đổi, và những kết quả gần đây trên các không gian với độ cong Ricci bị chặn dưới. Những bài giảng bên cạnh cung cấp những kiến thức nhập môn cũng dẫn dắt học viên tới những chủ đề nghiên cứu thời sự nhất, cũng như đề cập đến nhiều bài toán mở thú vị. Sự đa dạng của các bài giảng đã đáp ứng được nhu cầu của đông đảo học viên và giảng viên tham gia. Tất cả học viên và giảng viên đều tìm thấy cho mình nhiều bài học bổ ích, cũng như tìm được đối tác phù hợp để thảo luận và trao đổi các ý tưởng toán học.

Bên cạnh 2 tuần tham gia các bài giảng chính, các học viên và giảng viên của Trường hè được tham dự Hội thảo “Một số vấn đề của hình học vi phân đương đại” với sự tham gia thảo luận của các Giáo sư đầu ngành và một số các nhà toán học trẻ như GS. R. Schoen (UCI, Mỹ), GS. Bourguinon (IHES, Pháp), GS. S. Ohta (Osaka, Nhật Bản), TS. T. Buttsworth (Queensland, Úc), TS. Nguyễn Minh Hoàng (Vietnam National University, Hà Nội), TS. Gunhee Cho (UCSB, Mỹ). Các báo cáo viên đã thảo luận nhiều bài toán và kết quả thú vị trên các không gian và thời gian Finsler có trọng, các kết quả gần đây về lý thuyết mặt cực tiểu ổn định trong các đa tạp đối chiều cao, sự liên kết giữa vật lý và toán học thông qua các cấu trúc spinor, các kỹ thuật Bochner mới gần đây và ứng dụng nghiên cứu tính chất định dạng của các đa tạp, và cách xây dựng các xuyến cực tiểu trong các nhóm tuyến tính đặc biệt xạ ảnh. Đây là cơ hội cho các nhà nghiên cứu tham luận trực tiếp về các kết quả mới nhất về một số chủ đề của Hình học vi phân đương đại, thảo luận các phương pháp tiếp cận các bài toán mới, trao đổi các ý tưởng làm việc, mở rộng hợp tác trong lĩnh vực Hình học vi phân, đồng thời đem đến cho các sinh viên, học viên cao học trẻ một cơ hội để tiếp cận những thông tin mới nhất, làm quen với những chuyên gia hàng đầu, tìm hiểu thông tin và tiếp cận các hướng nghiên cứu để tìm kiếm các cơ hội học bổng học tập.
VIASM tin rằng Trường hè và hội nghị sẽ tạo ra một cơ hội đặc biệt để phát triển, và gợi cảm hứng cho các thế hệ trẻ tiếp tục nghiên cứu Hình học vi phân, một lĩnh vực quan trọng không chỉ trong khía cạnh lý thuyết mà trong cả ứng dụng. Chúng tôi trân trọng sự tham gia tích cực của các nhà nghiên cứu, chuyên gia và học viên trong và ngoài nước cũng như sự tài trợ của các tổ chức toán học thế giới. Tất cả các yếu tố này cùng đóng góp vào sự thành công của trường hè và hội thảo.